Introduction
Trapped ions are an excellent platform for scalable quantum information processing. A quantum bit or qubit can be formed by two suitable energy levels of an ion. It can be manipulated using laser beams. In the language of quantum information processing, this is called a single-qubit gate operation.
Besides these single-qubit gate operations, we require multi-qubit gate operations which change one qubit conditioned on the state of another. When multiple ions are cooled and trapped in a common potential, the Coulomb repulsion between them leads to the formation of so-called "Coulomb crystals". In these crytals, the Coulomb repulsion between the ions is balanced exactly by the restoring force of the trap potential which tries to squeeze the ions together. The joint motion of the ions in this crystal is an oscillation around the equilibrium position. Multi-qubit gates can be realized through additional laser beams which can "flip" individual quantum bits can be "flipped" together with an excitation or deexcitation of the ion crystal's oscillation ("motional sideband transitions"). This is the essence of the Cirac-Zoller proposal for quantum information processing with trapped ions [1]. One may also think of these multi-qubit gates as an effective spin-spin interaction [2] because a qubit is fully analogous to a spin 1/2.
Our goal is to contribute to the development and application of scalable methods for trapped-ion quantum information processing. In particular, we aim to exploit the analogy between qubits and spin 1/2 particles to implement interacting spin Hamiltonians and to study their properties. Already for moderate numbers of ions, it will be possible to implement Hamiltonians which are very difficult to simulate even on a supercomputer. Such "quantum simulations" could soon show a break even of quantum technlogy with classical supercomputing power.






Surface-electrode ion trap
We trap ions in Paul traps, where the confining force is given by combinations of static and oscillatory electric fields. We focus on surface-electrode ion traps [3], where all electrodes of the trap are located in a plane, and the ions are trapped above the surface. Miniature surface-electrode traps can be produced using scalable microfabrication techniques which have been developed in the context of microelectronics.
We produce our traps at PTB's clean room facility and at LNQE. Trap chips are made by coating an electrically insulating substrate with a thin titanium adhesion and gold seed layer. On top of the latter, we spin photoresist, expose the photoresist with a mask and develop the resist. In all the areas where the developer has removed the resist, we electroplate a ~10µm thick metal film. The remaining resist is removed subsequently together with the adhesion and seed layer underneath it. As a result, we obtain metal structures with 10 µm thick gold, separated by ~4µm wide gaps for electrical isolation between electrodes.
Surface-electrode traps are a great way to scale ion trap quantum information techniques because of reproducibility and because sophisticated trap arrays can be built up from individual trap "modules" and procued in a single production run on one substrate.
Loading single ions
We load single 9Be+ ions into our traps "at the push of a button" by sending a single nanosecond pulse onto a Beryllium wire. This releases a jet of neutral atoms across the trap surface [4]. A laser beam at 235 nm [5] provides enough energy to ionize a neutral atom through a two-photon ionization process. If the ion is created inside the trap volume, it is cooled and detected by a 313 nm laser beam [6] and its fluorescence is imaged onto a CCD camera, where the ion appears as a bright spot.



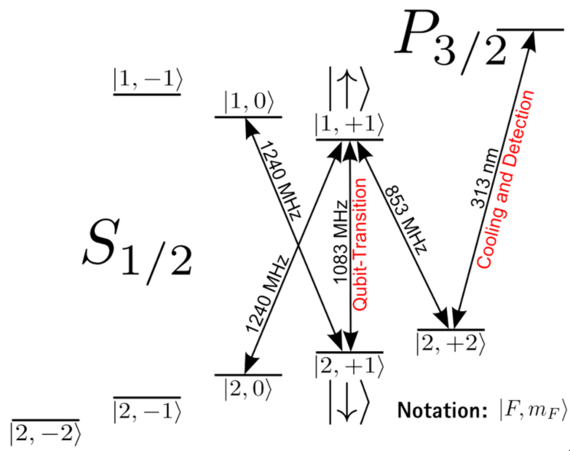
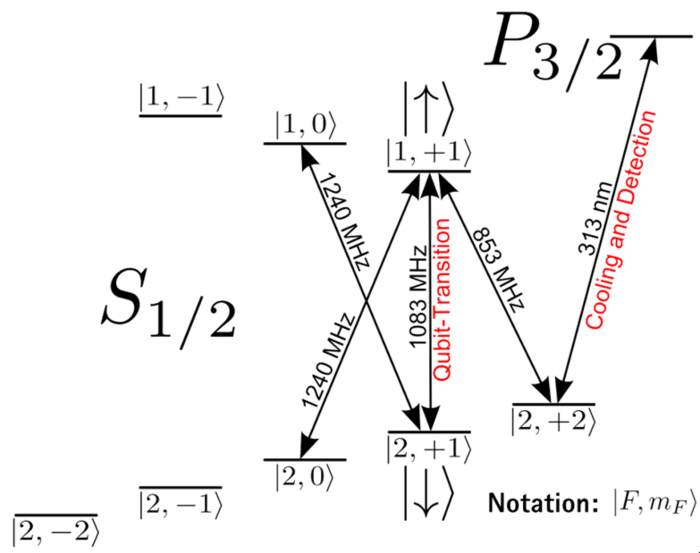
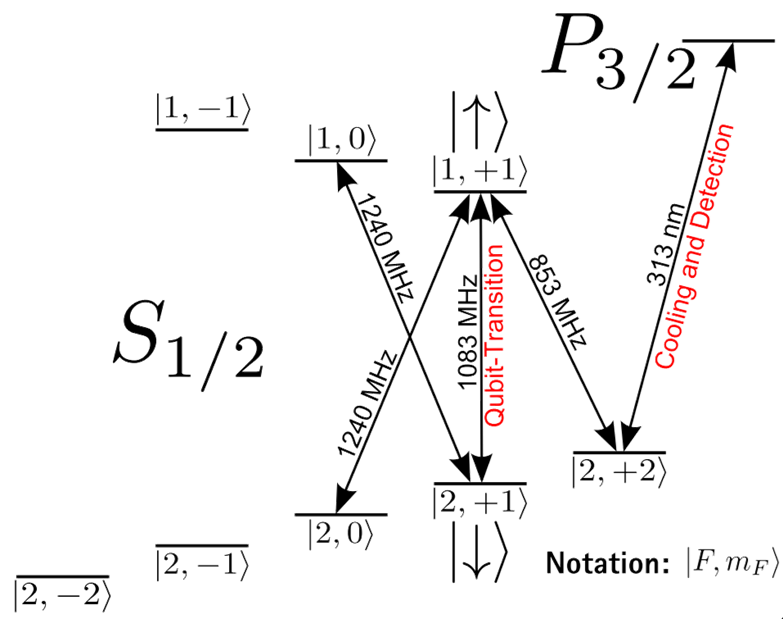
Field-independent qubit for long coherence times
We trap the ion at a magnetic field of 223 G between the Zeeman and Paschen-Back regimes. At this value of the magnetic field, the transition between the hyperfine states |F = 2, mF = 1> and |F = 1, mF = 1> in the electronic ground state is first order magnetic-field independent, and we use these two states as |0> and |1> states for our qubit. The transition frequency between these two levels is ~1084 MHz.
The magnetic-field indpendence should lead to a long coherence time of the qubit states because magnetic field noise will not affect the transition frequency to first order. On similar transitions, coherence times of many tens of seconds have been observed in other groups [7,8]. Gate operation times, on the other hand, are of order 10 to 100 µs, so that many operations can be carried out during the coherence time of the qubit.
Microwave near-field control
In most experiments to date, laser fields have been used to control the qubits and realize quantum logic operations. We use a different ("microwave near-field") approach, developed by Christian Ospelkaus while at NIST. In this approach, a microwave field near-resonant with the qubit transition at 1083 MHz is used to control the qubits [9-14]. Because the field needs to exert a force on the ion to excite the joint motion of the Coulomb crystal for multi-qubit operations, the field needs to have a strong amplitude gradient.
Such an amplitude gradient can be created by sending the ~1083 MHz signals through a conductor embedded into the ion trap structure. The near-field decay of the magnetic field then leads to a strong amplitude gradient at the position of the ions a few tens of microns from the trap surface.
The benefit of this approach is:
- Lasers are only required for Doppler cooling and qubit state detection for fluorescence imaging. These laser systems are low power and not critical in their parameters.
- Spontaneous emission as a fundamtental source of decoherence inherent to all laser-based schemes is completely eliminated.
- Operations should be much less sensitive to the motional state of the ions, so that cooling requirements could be reduced.
- The "hardware" that manipulates the qubits becomes part of the trap structure, unlike a sophisticated external laser system covering several square meters of optical table space. By virtue of microfabrication, a structure that realizes a given operation on ion qubits could be replicated many times in a given trap array.
- Microwave fields should be less difficult to control than laser beams. This is important for reaching low gate errorrates, where quantum error correction could be applied efficiently.
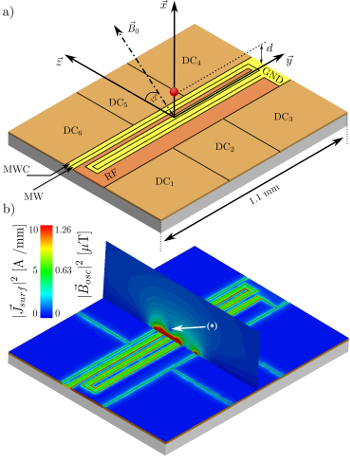




Microwave near-field design
The efficiency of the microwave near-field approach critically depends on the spatial properties of the microwave fields. For multi-qubit operations, we require a structure which produces a small microwave magnetic field amplitude at the location of the ions, but a large amplitude gradient. We have developed highly accurate numerical techniques to design suitable structures. This is a challenging task because any microwave current flow in the trap structure will lead to induced eddy currents which alter the fields. In the figure below, one can see a microwave conductor (MW) layed out in the form of an extremely compressed
"S" which will generate such a field. The lower part of the picture shows the surface current density in the strucure, and one can clearly identify the eddy currents which affect the near-field.
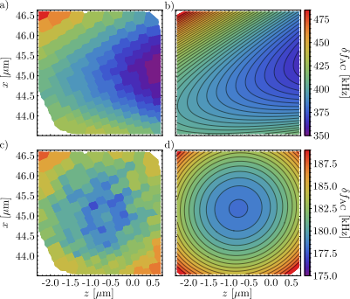
By trapping a single ion above the surface, we can measure the field distribution of the near-field as a function of position through energy shifts ("AC Zeeman shifts") which the near-field produces for the atomic energy levels. The figure below shows experimentally measured energy shifts (color coded) as a function of position for two different atomic hyperfine transitions. We have developed a suitable parameterization of microwave near-fields and fitted this model to the experimental data (right column). The location of the magnetic near-field minimum agree with our numerical simulations at the sub-µm level, and the angles characterizing the spatial orientation and polarization of the fields at the level of a few degrees only. This is a remarkable agreement for this regim of centimer waves localized to a few tens of microns.
Towards quantum many-body physics in trap arrays
In the future, we plan to extend our single-zone trap to multi-zone trap arrays. One possible application of these trap arrays is to realize systems of many interacting spins, represented by qubits in individual microtraps [2]. By shaping of the potentials and couplings in each individual microtrap, in principle arbitrary spin-spin interactions could be realized. By exploiting coupling to the motional modes and additional optical fields, coupling to bosonic degrees of freedom can be added and controlled dissipation may be introduced into the system.
References
- [1] J. I. Cirac and P. Zoller, Phys. Rev. Lett. 74, 4091 (1995).
- [2] D. Porras and J. I. Cirac, Phys. Rev. Lett. 92, 207901 (2004).
- [3] S. Seidelin et al., Phys. Rev. Lett. 96, 253003 (2006).
- [4] R. J. Hendricks et al., Appl. Phys. B 88, 507 (2007).
- [5] H.-Y. Lo et al., Appl. Phys. B 114, 17 (2013).
- [6] A. C. Wilson et al., Applied Physics B 105, 741 (2011).
- [7] C. Langer et al. Phys. Rev. Lett. 95, 060502 (2005).
- [8] T. P. Harty et al., Phys. Rev. Lett. 113, 220501 (2014).
- [9] C. Ospelkaus et al., Phys. Rev. Lett. 101, 090502 (2008).
- [10] C. Ospelkaus et al., Nature 476, 181 (2011).
- [11] K. R. Brown et al., Phys. Rev. A 84, 030303 (2011).
- [12] U. Warring et al., Phys. Rev. Lett. 110, 173002 (2013).
- [13] U. Warring et al., Phys. Rev. A 87, 013437 (2013).
- [14] C. Ospelkaus, U. Warring, and Y. Colombe, Physik in Unserer Zeit 45, 72 (2014).
- [15] M. Carsjens et al., Appl. Phys. B 114, 243 (2014).


